https://www.acmicpc.net/problem/10844
10844번: 쉬운 계단 수
첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
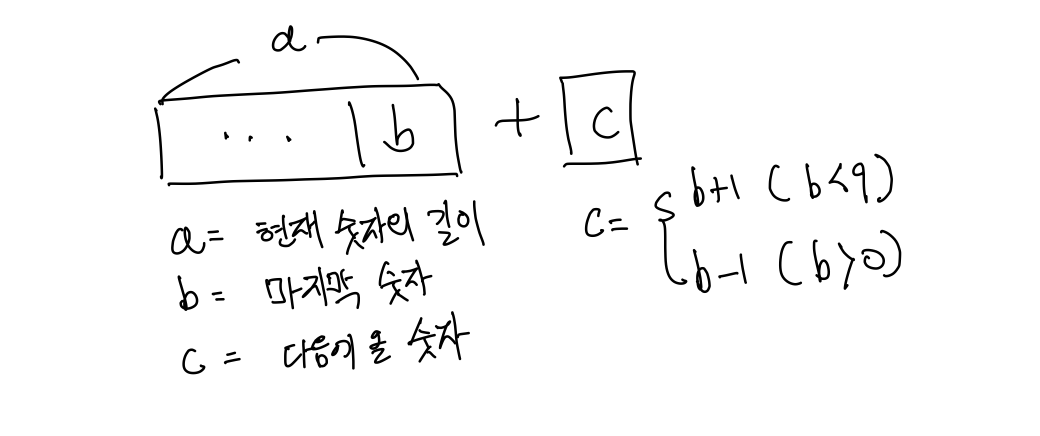
위 노트를 보면서 간단하게 설명해보겠습니다.
만약 길이가 a 이고 마지막 숫자가 b 인 수가 있습니다. 다음숫자인 c는 어떤 숫자가 와야할까요?
c 는 b가 9보다 작다면 b+1이 와야하고 b가 0보다 크다면 b-1이 올 수 있습니다.
예를 들어, b=8인경우를 생각해보겠습니다. 그러면 다음에 올 수 있는 숫자는 7과 9입니다.
b=0인 경우를 생각하면 다음에 올 수 있는 숫자는 1 밖에 없습니다.
b=9인 경우는 다음에 올 수 있는 숫자는 8 밖에 없습니다.
위 내용을 바탕으로 점화식을 세워 볼겁니다.
먼저 점화식을 세울 2차원 배열을 dp 로 선언합니다.
dp[i][j] 의 의미는 "길이가 i 이고 마지막 숫자가 j 인 계단수의 개수" 입니다.
이런 방식으로 점화식을 세우면 아래와 같습니다.
/*
dp[i][j] 의 의미는 길이가 i 이고 마지막 숫자가 j 인 계단수의 개수 입니다.
*/
dp[i][j] = {
dp[i][j+1] (j<9인 경우) + dp[i][j-1] (j>0인 경우)
}
식을 세웠으면 첫째항을 정합니다.
dp[1][0] = 0 (0부터 시작하는 계단수는 없다고 문제에서 명시 )
dp[1][1] = 1
dp[1][2] = 1
..
dp[1][9] = 1
점화식을 코드로 변환해보겠습니다.
if(j < 9 ) dp[i][j] += dp[i][j+1];
if(j > 0 ) dp[i][j] += dp[i][j-1];위 코드를 삼항 연산자로 나타내보겠습니다.
dp[i][j] += (j>0 ? dp[i-1][j-1] : 0 ) + ( j<9 ? dp[i-1][j+1] : 0 );여기서 MOD 로 나눠줘야 하기 때문에 MOD를 추가하겠습니다.
dp[i][j] = (dp[i][j] + (
(j>0 ? dp[i-1][j-1] : 0) +
(j<9 ? dp[i-1][j+1] : 0)
)%MOD )%MOD;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
/**
* Main 설명 : 쉬운 계단 수
* @author jowonjun
* @version 1.0.0
* 작성일 : 2022/03/17
**/
public class Main {
static Fs fs = new Fs();
static int MOD = 1_000_000_000;
static int[][] dp = new int[101][10];
public static void main(String[] args) throws Exception {
int n = fs.nInt();
/**
* dp[i][j] -> i= 길이 , j = 마지막으로 끝난 수
*
* dp[i][j] = dp[i-1][j-1] + dp[i-1][j+1]
*
*/
for(int i=1;i<=9;i++) dp[1][i] = 1; // 0 으로 시작하는 수는 계단 수가 아님.
for(int i=2;i<=100;i++) {
for(int j=0;j<=9;j++) {
dp[i][j] = (dp[i][j] + (
(j>0 ? dp[i-1][j-1] : 0) +
(j<9 ? dp[i-1][j+1] : 0)
)%MOD )%MOD;
}
}
long sum = 0;
for(int i=0;i<10;i++) sum = (sum + dp[n][i])%MOD;
System.out.println(sum);
}
static class Fs{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer("");
public int nInt() throws Exception{
if(!st.hasMoreTokens()) st= new StringTokenizer(br.readLine());
return Integer.parseInt(st.nextToken());
}
}
}'algorithm' 카테고리의 다른 글
| [JAVA] 백준 1379 와 세제곱 (백트래킹 , 정수론) (0) | 2022.03.19 |
|---|---|
| [JAVA] 백준 변형 계단수 18244 (다이나믹프로그래밍) (0) | 2022.03.18 |
| [JAVA] 2021 카카오문제 - 메뉴 리뉴얼 (0) | 2022.03.15 |
| [JAVA] 백준 K번째 최단경로 찾기 1854 (다익스트라) (0) | 2022.03.12 |
| [JAVA] XOR 연산자 ^ 에 대해 ( feat. 백준 - XOR (12844번)) (0) | 2021.03.20 |


댓글