- 위상정렬이란?
순서가 정해져 있는 작업들의 목록들을 가지고 전체 작업 순서를 결정하도록 하는 알고리즘. 이를 위해서는 사이클이 없는 방향그래프에서만 해야한다. 아래 그래프로 예를 들겠다.
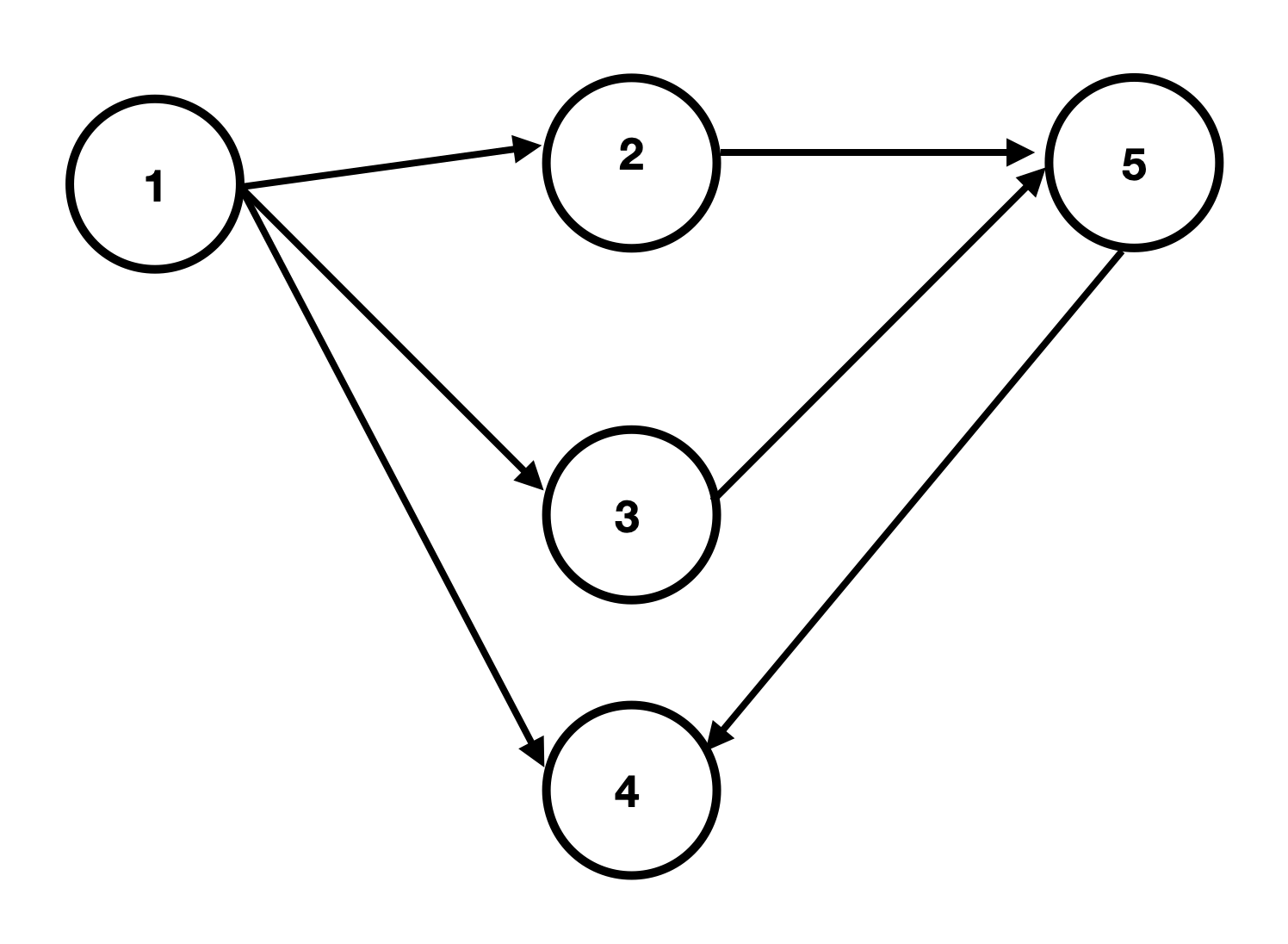
1번 작업은 2번보다 먼저 해야한다. 이것을 방향그래프로 나타내었다. 2번은 5번 보다 먼저 해야 한다. 5번은 4번 보다 먼저 해야한다. 만약 위와 같은 작업 스케줄이 있다면 어떻게 진행하면 좋을 것인가?
1 - 2 - 3 - 5 - 4
1 - 3 - 2 - 5 - 4
위 2가지 경우중에서 한가지 선택하여 진행하면 된다.
먼저 차수에 대해 정의하겠다.
한 정점의 차수 = 해당 정점보다 먼저 선행되어야 하는 작업의 수
예를들어, 3번의 차수는 1이다. 1번 작업이 선행되어야 하기 때문이다.
5번의 차수는 2이다. 2번과 3번의 작업이 선행되어야 하기 때문이다.
이제 위상정렬의 알고리즘에 대해 소개한다.
해당 알고리즘은 m.blog.naver.com/ndb796/221236874984
25. 위상 정렬(Topology Sort)
위상 정렬(Topology Sort)은 '순서가 정해져있는 작업'을 차례로 수행해야 할 때 그 순서를 결정해주기 ...
blog.naver.com
나동빈님 코드를 참조하여 JAVA 코드로 작성해 볼것이다.
- 위상정렬 알고리즘
1번부터 n번까지 정점이 존재한다고 가정한다. 또한 사이클이 없는 방향그래프라고 가정한다. ( 큐가 비었는지 안비었는지 검사 안할 것임)
1. 차수가 0인 모든 정점을 큐에 넣는다. (선행되어야 하는 정점이 없는 정점이다.)
2. 2-1 ~ 2-4 를 n번 반복한다. (n 개의 정점을 꺼낼 것임! )
2-1. 큐에서 하나를 꺼낸다. 꺼낸 정점을 x라고 한다.
2-2. x를 전체 작업순서에 추가한다. ( 본인은 StringBuilder 에 apppend 함)
2-3. x 다음에 작업해야하는 모든 정점의 차수를 감소시킨다.
2-4. 차수가 감소된 정점이 0이라면 큐에 넣는다.
- 위상 정렬 예시
위 그래프로 예시를 들어 보겠다. 참고로 색칠된 정점은 큐에 있는 정점을 표시한 것이다. 그 이상의 의미는 없다. Degree에 빨간색으로 제거한 것은 차수가 0인 정점을 표시한것으로 그 이상의 의미는 없다.
1. degree가 0인 1을 큐에 넣는다.

2. 큐에서 하나 꺼낸다. 1번 다음에 작업해야되는 정점들의 차수를 1씩 모두 감소시킨다(= 간선없애는 작업이라고 보면됨). 감소시킨 차수가 0이면 모두 큐에 넣는다.
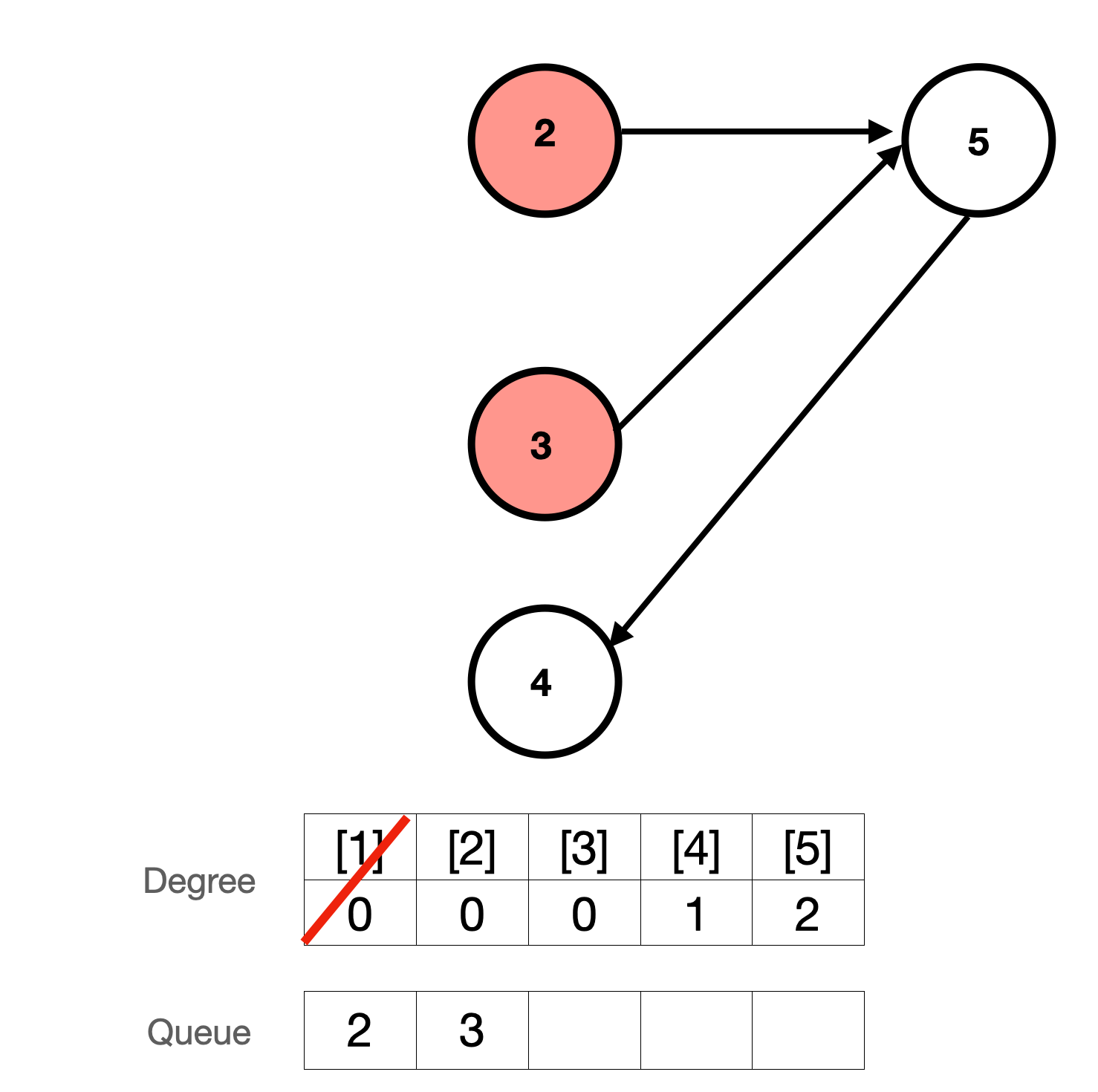
3. 큐에서 하나 꺼낸다. 2번 정점 다음에 작업해야하는 정점의 차수를 감소시킨다. 감소시킨 차수가 0이면 큐에 넣어야하는데 5번 정점의 차수르 1 감소해도 0이 아니므로 그냥 넘어간다.
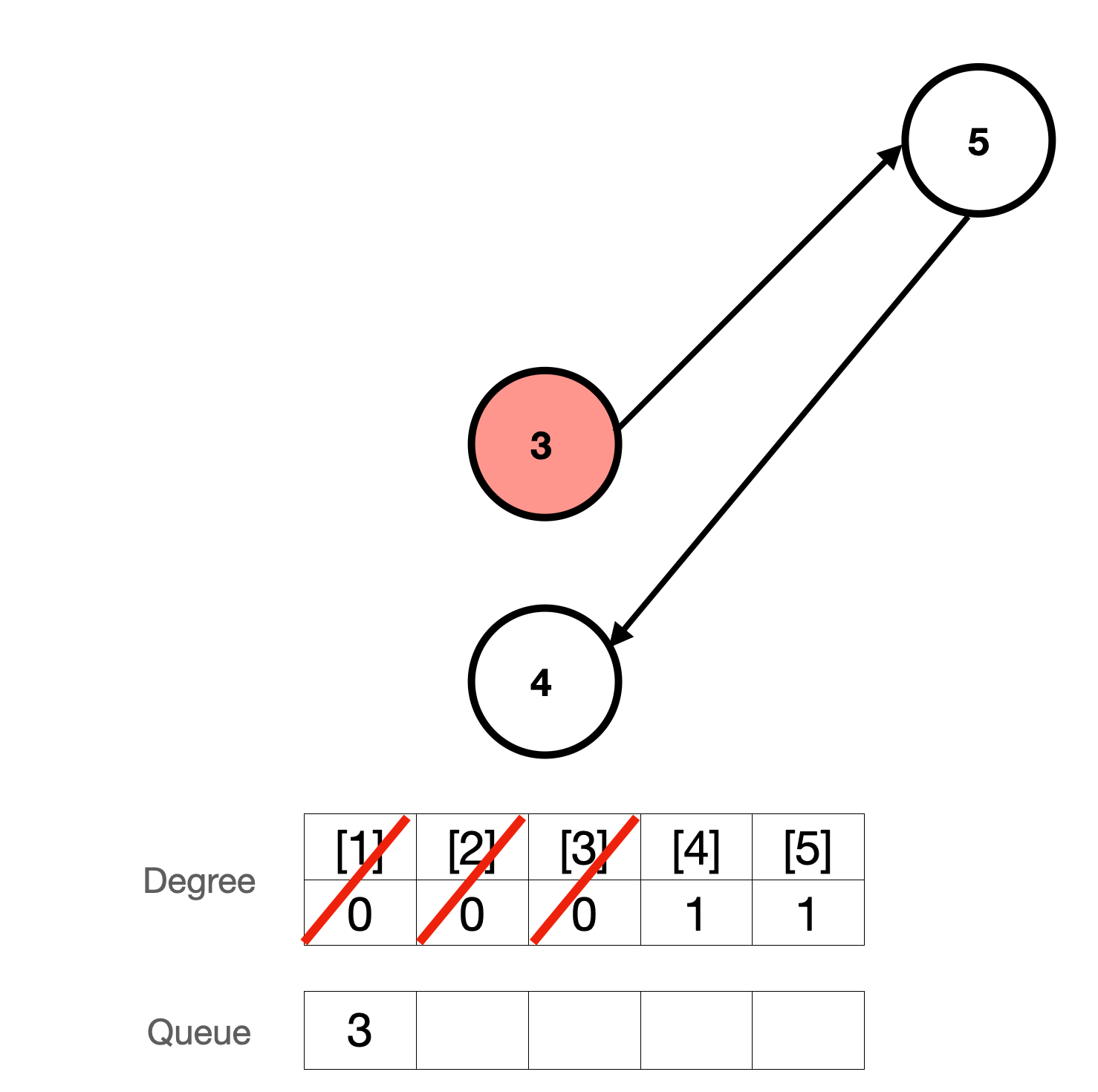
4. 큐에서 하나 꺼낸다. 3번 다음에 수행해야하는 5번의 차수를 1감소시킨다. 그리고 5번의 차수가 0이므로 큐에 넣는다.
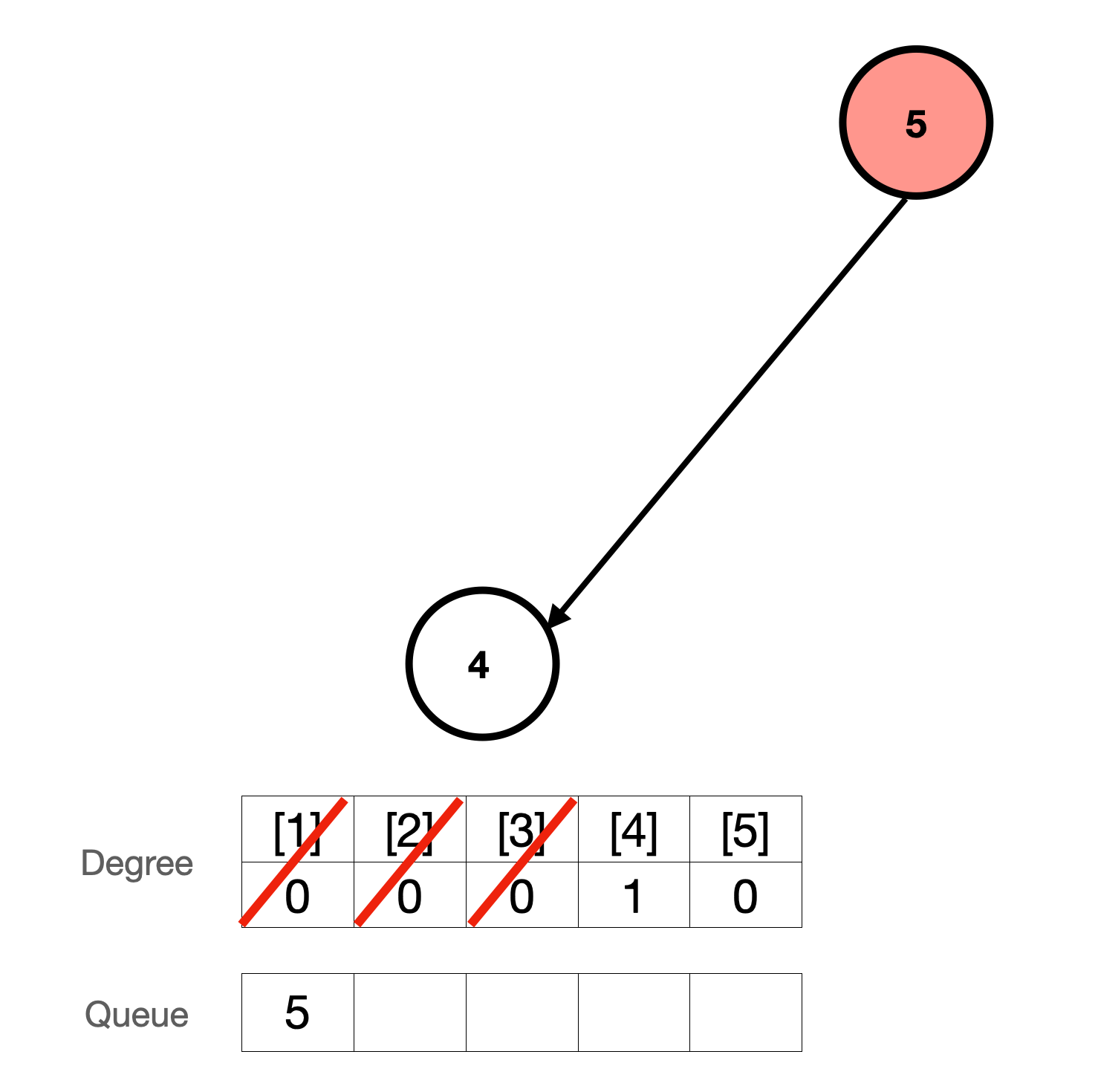
5. 큐에서 하나 꺼낸다. 5번 다음에 수행해야하는 4번의 차수를 1 감소시키고 4번 정점의 차수가 0이므로 큐에 넣는다.
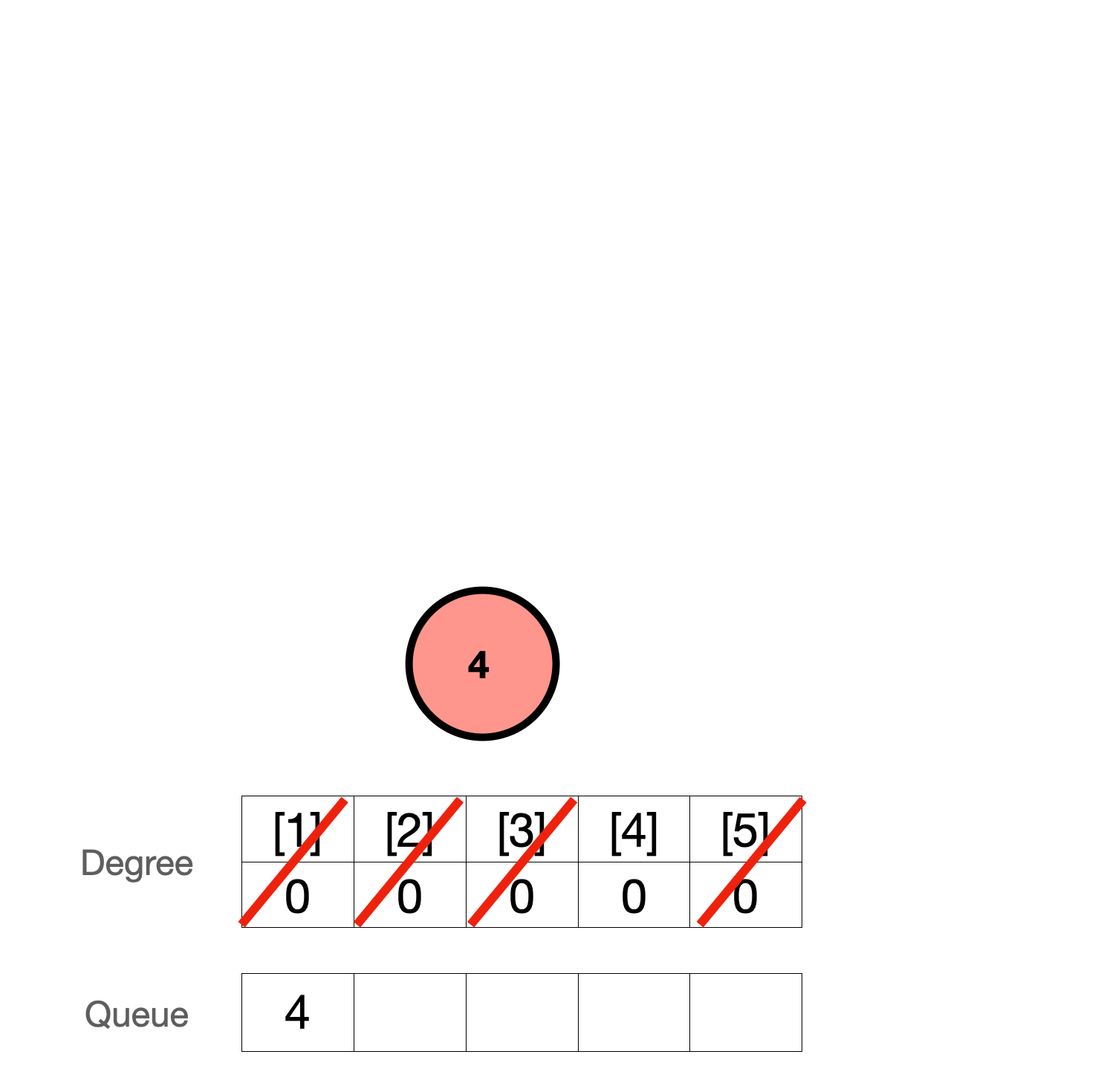
5. 큐에서 4번을 꺼낸다. 다음 수행해야할 작업이 없으므로 끝.
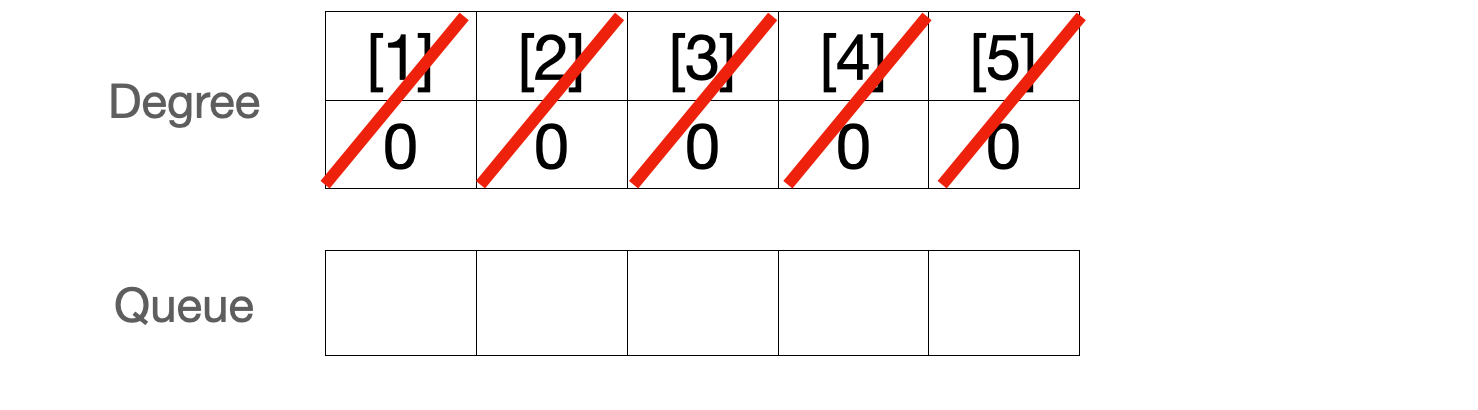
6. 큐에서 꺼낸 순서대로 StringBuilder에 넣어주면 1 - 2 - 3 - 5 - 4 가 전체 작업순서가 된다.
- 문제 풀어보기
2252번: 줄 세우기
첫째 줄에 N(1≤N≤32,000), M(1≤M≤100,000)이 주어진다. M은 키를 비교한 회수이다. 다음 M개의 줄에는 키를 비교한 두 학생의 번호 A, B가 주어진다. 이는 학생 A가 학생 B의 앞에 서야 한다는 의미이
www.acmicpc.net
<자바코드>
import java.io.*;
import java.util.*;
public class Main {
static int n,m;
static int[] degree;
static StringBuilder sb = new StringBuilder();
static ArrayList<Integer>[] a;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
a = new ArrayList[n+1];
for(int i=1;i<=n;i++) a[i] = new ArrayList<>();
degree = new int[n+1];
int t1,t2;
for(int i=0;i<m;i++){
st = new StringTokenizer(br.readLine());
t1 = Integer.parseInt(st.nextToken());
t2 = Integer.parseInt(st.nextToken());
// t1 다음에 t2 수행해야됨.
a[t1].add(t2);
// t2 의 차수를 1증가 시킨다.
degree[t2]++;
}
// 위상정렬
topologySort();
System.out.println(sb);
}
static void topologySort(){
Queue<Integer> q = new LinkedList<>();
// 차수가 0인 정점 큐에 넣기 (선행되어야할 작업이 없는 정점임)
for(int i=1;i<=n;i++){
if(degree[i]==0)
q.add(i);
}
// n번 루프를 돌며 총 n개의 정점에 대해 작업함. 1부터 n까지 순서의 의미보다는 n번 반복한다는 의미로 받아들어야함.
for(int i=1;i<=n;i++){
int x = q.poll();
sb.append(x).append(" ");
// 정점x 다음에 작업해야하는 conn 의 차수를 1감소시킨것이 0이라면 큐에 conn을 넣는다.
for(int conn : a[x]) {
if(--degree[conn] == 0){
q.add(conn);
}
}
}
}
}
1005번: ACM Craft
첫째 줄에는 테스트케이스의 개수 T가 주어진다. 각 테스트 케이스는 다음과 같이 주어진다. 첫째 줄에 건물의 개수 N 과 건물간의 건설순서규칙의 총 개수 K이 주어진다. (건물의 번호는 1번부
www.acmicpc.net
<자바 코드>
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
static int tt;
static int n,k;
static int w;
static int[] times;
static int[] degree;
static int[] res;
static ArrayList<Integer>[] arr;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
tt = Integer.parseInt(st.nextToken());
while(tt-- != 0 ){
st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
k = Integer.parseInt(st.nextToken());
times = new int[n+1];
degree = new int[n+1];
res = new int[n+1];
arr = new ArrayList[n+1];
for(int i=1;i<=n;i++) arr[i] = new ArrayList<>();
st = new StringTokenizer(br.readLine());
for(int i=1;i<=n;i++) times[i] = Integer.parseInt(st.nextToken());
int temp1,temp2;
for(int i=1;i<=k;i++){
st = new StringTokenizer(br.readLine());
temp1 = Integer.parseInt(st.nextToken());
temp2 = Integer.parseInt(st.nextToken());
arr[temp1].add(temp2);
degree[temp2]++;
}
st = new StringTokenizer(br.readLine());
w = Integer.parseInt(st.nextToken());
topologySort();
System.out.println(res[w]);
}
}
static void topologySort(){
Queue<Integer> q = new LinkedList<>();
for(int i=1;i<=n;i++){
if(degree[i]==0) {
res[i] = times[i];
q.add(i);
}
}
for(int i=1;i<=n;i++){
int x = q.poll();
for(int next : arr[x]){
if(res[next] < res[x] + times[next]){
res[next] = res[x] + times[next];
}
if(--degree[next] == 0){
q.add(next);
}
}
}
}
}
'algorithm' 카테고리의 다른 글
| [JAVA] 세그먼트 트리 ( SegmentTree ) (0) | 2021.03.07 |
|---|---|
| [JAVA] 백준 - 캐슬 디펜스 17135 (테케 다 맞는데 틀린다면?) (0) | 2021.03.04 |
| [JAVA] 백준 1707 - 이분 그래프 (0) | 2021.02.23 |
| [JAVA] 백준 7562 - 나이트의 이동 ( BFS) (0) | 2021.02.18 |
| [JAVA] 백준 2583 - 영역구하기 ( BFS + 구현 ) (0) | 2021.02.15 |
댓글