2458번: 키 순서
1번부터 N번까지 번호가 붙여져 있는 학생들에 대하여 두 학생끼리 키를 비교한 결과의 일부가 주어져 있다. 단, N명의 학생들의 키는 모두 다르다고 가정한다. 예를 들어, 6명의 학생들에 대하여
www.acmicpc.net
플루이드 외샬 알고리즘을 적용하면 빠르게 풀 수 있는데 나는 쓰지 않았다.
BFS 를 쓰면 더 빠를 거라고 생각했기 때문이다. 실제로 더 빨라서 전체 백준 차트에서 2등했다. (물론 메모리를 좀더 쓰긴 했지만..)
(2020.02.13 기준)

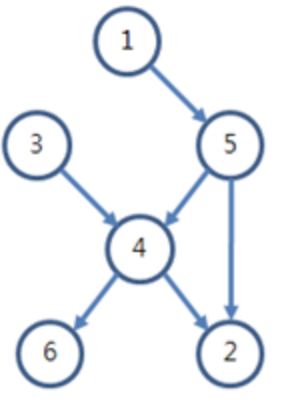
BFS 풀이법
- 1번 정점에서 BFS를 시작하여 1번보다 큰 정점을 체크한다. 여기서는 2,4,5,6번이 체크된다.
- 2번 정점에서 BFS를 시작하여 1번보다 큰 정점을 체크한다. 여기서는 아무것도 체크되지 않는다.
- 3번 정점에서 BFS를 시작하여 1번보다 큰 정점을 체크한다. 여기서는 2,4,6번이 체크된다.
- 4번 정점에서 BFS를 시작하여 1번보다 큰 정점을 체크한다. 여기서는 2,6번이 체크된다.
- 5번 정점에서 BFS를 시작하여 1번보다 큰 정점을 체크한다. 여기서는 2,4,6번이 체크된다.
- 6번 정점에서 BFS를 시작하여 1번보다 큰 정점을 체크한다. 여기서는 아무것도 체크되지 않는다.
위 정보를 arr라는 2차원 정보에 저장한다.
예를들어 arr[1][2] = 1 이면 "1번 정점에서 2번 정점으로 갈 수 있다" 는 의미다.
arr는 아래와 같이 나타난다. 1번 정점 부터 6번 정점까지의 상황이다.
arr[i][j] = 1 이면 i에서 j까지 갈 수 있다는 의미 즉, i보다 j가 키가 크다는 의미다.

위 arr에서 각각의 정점에 대한 모든 1을 더해서 n-1 인지 체크해주면 된다.
무슨 말이냐면, arr[1][i] 에서 (i 는 1부터 6까지의 수) arr[1][i]=1 이면 1번 정점보다 키가 큰 i 가 있다는 의미다.
arr[i][1] 에서 (i는 1부터 6까지의 수) arr[i][1]=1 이면 1번 정점보다 키가 작은 i가 있다는 의미다.
따라서 arr에서 각각의 정점에 대해 모든 1을 카운트하여
자신보다 작은 사람 수 + 자신보다 큰 사람의수 = n -1 (전체에서 본인제외)
를 구하면 된다.
<전체 코드>
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
static int n,m;
static boolean[][] arr = new boolean[501][501];
static int[] isRanked = new int[501];
static int ans;
public static void main(String[] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
int a,b;
for(int i=0;i<m;i++){
st = new StringTokenizer(br.readLine());
a = Integer.parseInt(st.nextToken());
b = Integer.parseInt(st.nextToken());
arr[a][b] = true;
}
for(int i=1;i<=n;i++)
bfs(i);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(arr[i][j]) isRanked[i]++;
if(arr[j][i]) isRanked[i]++;
}
}
for(int i=1;i<=n;i++){
if(isRanked[i] == n-1){
ans++;
}
}
System.out.println(ans);
}
static void bfs(int start){
boolean[] visited = new boolean[501];
Queue<Integer> q = new LinkedList<>();
visited[start] = true;
q.add(start);
while(!q.isEmpty()){
int first = q.poll();
for(int i=1;i<=n;i++){
if(!visited[i] && arr[first][i]){
visited[i] = true;
arr[start][i] = true;
q.add(i);
}
}
}
}
}
'algorithm' 카테고리의 다른 글
| [JAVA] 백준 7562 - 나이트의 이동 ( BFS) (0) | 2021.02.18 |
|---|---|
| [JAVA] 백준 2583 - 영역구하기 ( BFS + 구현 ) (0) | 2021.02.15 |
| [JAVA] 백준 11404- 플로이드(플로이드-외샬 알고리즘이란?) (0) | 2021.02.08 |
| [JAVA] 전구와 스위치 (백준 2138) ( 그리디) (0) | 2020.10.23 |
| [JAVA] 백준 - 동전0 - 11047 (그리디) (0) | 2020.10.16 |


댓글